Another blast from the blog past! 2017 this time, and the question is "what do you see when you fall into a black hole?" There is a lot written about this out there on the internet, but some is confused, some is muddled, some is crazy. Here is my take.
---
Everyone loves black holes. Immense gravity, a one-way space-time membrane, the possibility of links to other universes. All lovely stuff.
A little trawl of the internets reveals an awful lot of web pages discussing black holes, and discussions about spaghettification, firewalls, lost information, and many other things. Actually, a lot of the stuff out there on the web is nonsense, hand-waving, partly informed guesswork. And one of the questions that gets asked is "What would you see looking out into the universe?"
Some (incorrectly) say that you would never cross the event horizon, a significant mis-understanding of the coordinates of relativity. Others (incorrectly) conclude from this that you actually see the entire future history of the universe play out in front of your eyes.
What we have to remember, of course, is that relativity is a mathematical theory, and instead of hand waving, we can use mathematics to work out what we will see. And that's what I did.
I won't go through the details here, but it is based upon correctly calculating redshifts in relativity and conservation laws embodied in Killing vectors. But the result is an equation, an equation that looks like this
Here, rs is the radius from which you start to fall, re is the radius at which the photon was emitted, and ro is the radius at which you receive the photon. On the left-hand-side is the ratio of the frequencies of the photon at the time of observation compared to emission. If this is bigger than one, then the photon is observed to have more energy than emitted, and the photon is blueshifted. If it is less than one, then it has less energy, and the photon is redshifted. Oh, and m is the mass of the black hole.
One can throw this lovely equation into python and plot it up. What do you get.
So, falling from a radius of 2.1m, we get
And falling from 3m
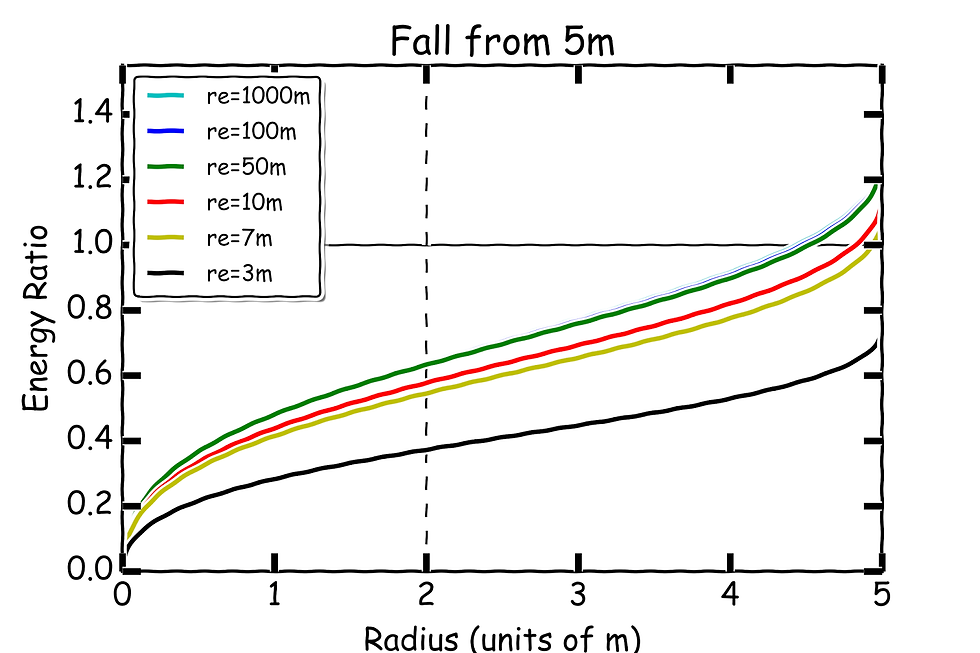
And from 5m
And 10m
and finally at 50m
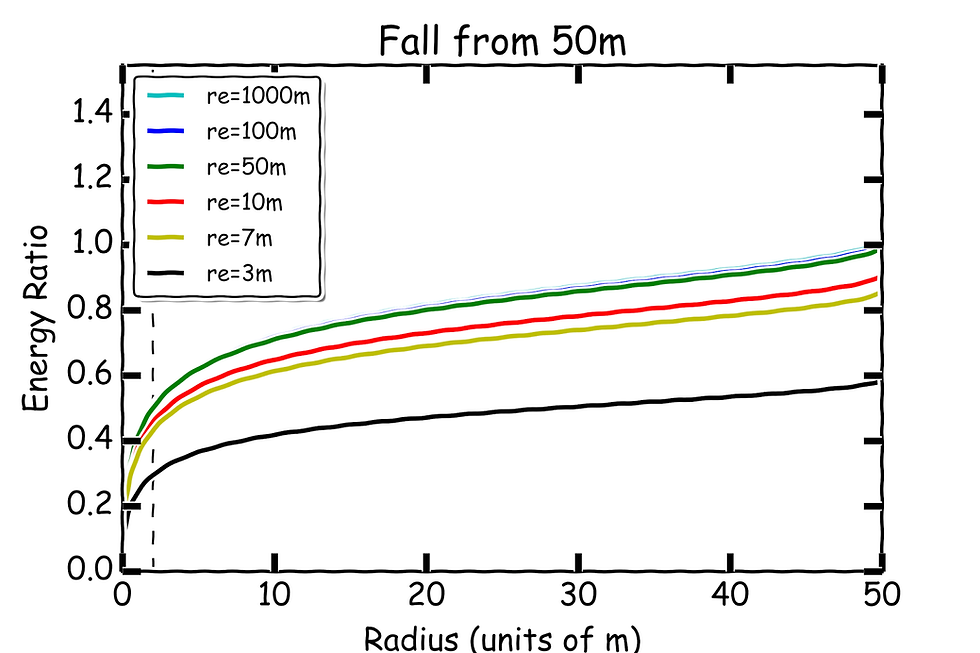
In each of these, each line is a photon starting from different differences.
The key conclusion is that within the event horizon (r=2m) photons are generally seen to be redshifted, irrespective of where you start falling from. In fact in the last moment before you meet your ultimate end in the central singularity, the energy of the observed photon goes to zero and the outside universe is infinitely reshifted and vanishes from view.
How cool is that?
---
A small subtlety not noted in the original post, but the equation above is really only valid when the faller is at a smaller radius than the source emitting the photons, so an inward falling observer encounters an inward falling photon. If the faller is at a larger radius that the source (so the infalling observer encounters an outward moving photon, the negative sign between the two first square roots becomes a positive. But more on that later.
Thinking about how things fall into black holes is really interesting and counterintuitive. One of my favourite bits of work I did was looking at what you could do with a rocket pack below the event horizon of a black hole. TL;DR no happy ending. You can read the paper here.
