Our old friend Veritasium posted this probability problem a while ago on what is apparently the trickiest problem of them all.
In the problem, Sleeping Beauty is the subject of an experiment. On Sunday, she is told she will be put to sleep and a coin tossed. If the coin comes up heads, she will be woken on Monday and then put back to sleep. If the coin comes up tails, she will be woken on Monday and put back to sleep, and then woken on Tuesday and put back to sleep again. Finally, she will be woken on Wednesday at the conclusion of the experiment.
When she is awake, she will be asked what the probability that the outcome of the coin flip was heads. She will then have her memory of the awakening wiped before she is put back to sleep.
The apparent argument is over whether this probability a third or a half. I scratched my head a little at this video, as the problem doesn't seem tricky at all.
The key point is that the probability that the coin coming up heads, and the probability of the coin coming up heads given that Sleeping Beauty was asked are two separate questions, and so they do not necessarily have to have the same answer.
Let's explore this using Bayes theorem.
So, this calculates the probability that the coin came up heads (H) given that Sleeping Beauty was asked (A). What about the other terms?
Well, P(H) is the probability that the coin came up heads. It's a fair coin, so P(H) = 1/2.
P(A) is the probability that sleeping beauty was asked. There are 4 opportunities for her to be asked. Irrespective of the outcome of the coin toss, then she could be asked on Monday or Tuesday. But if it was actually heads she is only asked once. So P(A) = 3/4.
What about P(A|H)? That is the probability that Sleeping Beauty is asked given that the coin came up heads. Clearly, P(A|H) = 1/2.
Putting this all together, P(H|A) = 1/3. There is no mystery.
Let's calculate P(T|A) to be sure. Again, using Bayes theorem we have:
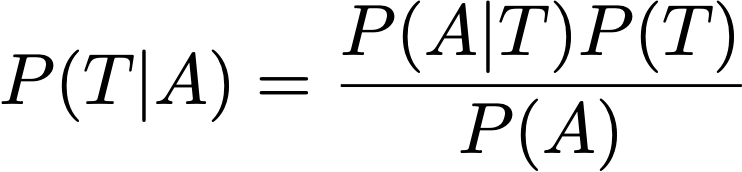
Again, looking at the other terms. P(T) = 1/2 - it's a fair coin after all. P(A) is still 3/4.
What about P(A|T)? If it came up tails, then she is guaranteed to be asked, so P(A|T)=1. Putting this all together, then P(T|A) = 2/3.
The moral of the story. The answer depends on the question that is asked, so make sure you ask the right question!